_770.webp)
Our reader, Den, created his system for playing roulette. He has been using it for years, gambling at least two or three times a week.
"Sometimes I'm nervous, but I never left a casino in the red in the previous year," - he says.
Has Den found a way to beat the casino? Is it theoretically possible? Let's find this out.
Conspiracy Theory
I have observed that all the major gambling websites emphasize that it is impossible to beat the casino when playing roulette. It has been mathematically proven that players who utilize any system while playing roulette will inevitably lose over time.
It’s always suspicious when everyone echoes the same sentiment. What benefits do casinos gain from this negative information that is consistently present in gambling resources? Are they being truthful? After all, if you repeat a lie long enough, it becomes accepted as the truth.

Once upon a time, there was a myth that people could never fly. Everyone believed it! However, balloons emerged and challenged this belief. Ultimately, on December 17, 1903, the Wright brothers dispelled this myth when their Flyer flew for 14 seconds, covering a total distance of 39 meters. In just a few seconds, they dismantled a centuries-old belief.
This article is not intended to dispel the myth that it is impossible to win while playing roulette, but I hope it will make you think. I invite our dear readers to test the system described below and come to their conclusions.
Things Familiar to Everyone
Anyone can win money at the roulette table. However, this is only feasible in the short term, as casinos always prevail in the long term. Consequently, every player seeks to outsmart a casino and create a system that enables them to profit over an extended period.
Since roulette first appeared, many systems have been developed. Each leads players to the same conclusion: casinos always win. However, some systems enable users to win more often than they lose.

Let's discuss a little bit of theory.
- If you flip a coin, there's a 50% chance that heads will appear.
- A 50% probability is also noted for tails. Due to the coin’s topography, one side is heavier than the other, resulting in a slight deviation from 50%. However, we will not consider this argument.
- Therefore, if you toss a coin one thousand times, tails will show up 500 times, and heads will also show up 500 times.
- Therefore, many players believe that if heads appear many times in a row, the probability of tails appearing becomes higher.
It is a misconception. Whenever you toss a coin, there is a 50% probability of either outcome.

The same scenario is seen in roulette:
Even if red comes up 10 times in a row, the probability of red appearing on the 11th spin remains the same as it was for the first: 18/37.
Nothing proves that a black number must follow ten red numbers. However, there is a law of large numbers. According to this law, as you increase the number of trials, the average of the results becomes more accurate and is less affected by luck. In other words, we can say that:
- Red numbers come up in 10 spins in a row;
- The red/black ratio in one hundred spins can be roughly 40-60;
- It becomes closer to 500-500 in 1,000 spins;
- If there are higher orders of magnitude, the difference between the appearance of red and black numbers is so minor that it is considered a statistical error.
The Dozens Betting System for Roulette
My friend Den says he loves money but doesn’t enjoy games of chance. He regularly visits Las Vegas casinos and plays this way: he bets on dozens.- Numbers from 1 to 12 form the first dozen.
- The second dozen includes numbers from 13 to 24.
- Numbers from 25 to 36 form the third dozen.

If he wins, he gets three bets. When he does not win, one bet is lost. According to the probability theory, he must win in 32.43% of cases.
You might wonder why this probability isn’t equal to 33.33%. The roulette wheel has 37 numbers, not 36. The 37th number is zero, which gives a house edge of 2.7% and reduces the probability of winning by 0.9%.
He only places bets when one of the dozens has not won in the recent five spins. He knows that the outcome of each round is independent of the others, yet he continues to play this way. When we asked him about it, he replied, "I feel calm." Well, let's assume that it’s a struggle against negative emotions :)
If he wins, he waits for the next opportunity to place a bet. If he loses, he places bets in the following manner:
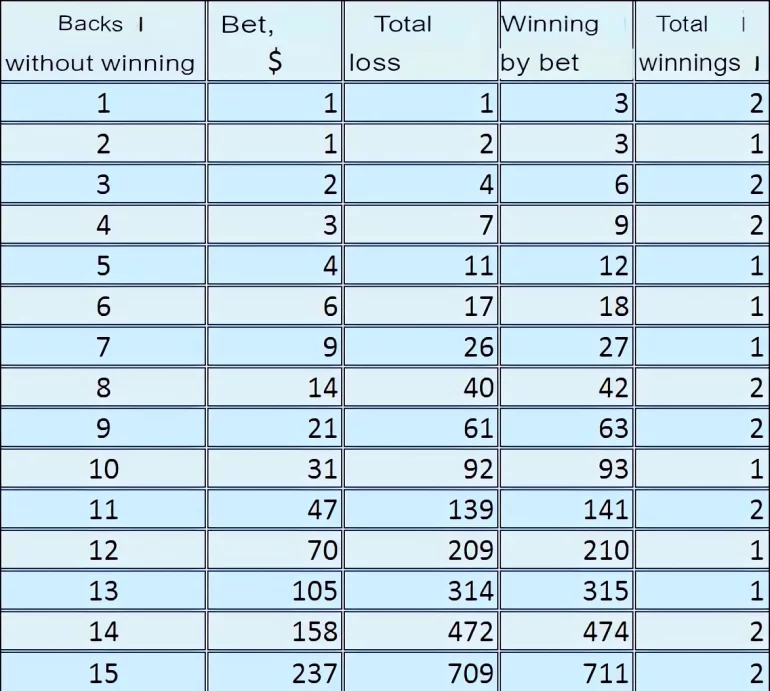
As we can see, his scheme resembles the infamous Martingale. Thus, he must take significant risks to win a substantial amount. However, I understand what causes Den to limit his sessions to 15 rounds: he hasn't placed the maximum bet in several years.
Let's calculate the probability that a particular dozen shows up at least once in 15 spins.
- The probability that a dozen comes up is 32.43% or 0.3243;
- The probability that a dozen does not come up is 100-32.43%=67.57% or 0.6757;
- The probability that a dozen does not come up 15 times in a row is 0.6757 to the power of 15 = 0.0028 or 0.28%;
- The probability that a dozen appears at least once in 15 spins is 1-0.0028=0.9972 or 99.72%.
Thus, according to the law of large numbers, he wins $1 or $2 in 9,972 out of 10,000 gaming sessions (note that we refer to sessions and not spins; each session can consist of 15 spins). The winnings may vary from $9,972 to $19,944. He may lose $709 on 28 occasions, making the total loss equal to $19,852.
As a result of 10,000 sessions, Den will likely be in the red; however, there is a slight chance of making a profit if you win $2 instead of $1 in each session.
Do you like online roulette? Check out these games.
Light Version
Nonetheless, $709 is a significant amount of money, and it’s unfortunate to lose it. Looking at the table, you might notice that if you reduce the session to 11 spins, you would only need to risk $139. Losing $139 doesn’t seem like a true disaster. Let's calculate the probabilities for 11 rounds:
- The probability that a dozen comes up is 32.43% or 0.3243;
- The probability that a dozen does not come up is 100-32.43%=67.57% or 0.6757;
- The probability that a dozen does not come up 11 times in a row is 0.6757 to the power of 11=0.0134 or 1.34%;
- The probability that a dozen appears at least once in 11 spins is 1-0.0134=0.9866 or 98.66%.
Therefore, 9,866 sessions will result in a positive outcome, while 134 will be negative out of 10,000. The winnings will range from $9,966 to $19,732. The total losses will amount to 134 x 139 = $18,626. If the number of spins is reduced to 11, the probability of winning increases by 1%. However, you risk losing an amount that is five times less than that in 15 spins. The theoretical probability of being profitable is still observed even with just 11 spins.
Pros and Cons of the Den's System
Den answers tricky questions well:
I understand casinos always win and don't pretend to hit the jackpot. While I know that theoretically, I should lose, fortunately, that hasn’t happened yet. The theory is intriguing, but I continue to win money and spend it. I renovated my home and bought a nice car. I can also afford to purchase various items. Even in theory, it seems complicated to lose all these things since I don’t make such hefty bets.
He claims he has never been affected by the table limits, which typically reach a few thousand dollars. He also mentions that he has only reached the 14th round once. However, he lost in the 13th round the previous year because he didn't have enough money to place a bet. "I was relaxed," Dan laughs. "I went to the casino with three hundred bucks and forgot my card at home."

Using this system to play roulette makes it impossible to beat the casino over time consistently. This holds for any other strategy as well. Nonetheless, the significant advantage of this system is that you will almost always win while playing roulette, resulting in a profit.
The drawbacks of Den's system include lower payouts compared to the bets. Another disadvantage is that losing sessions impact your bankroll more significantly than winning sessions. Additionally, you must have enough money to place a wager in the 15th round. Nevertheless, let's hope you never find yourself in that situation.
Should You Employ This Betting System?
This system is enjoyable for players because it allows for consistent wins. However, this approach requires excellent discipline and focus to follow the strategy and avoid confusing betting amounts. Ultimately, theoretically, you might lose, but that loss will be negligible.
You also have a chance of winning in the long run if your winnings consistently amount to $2. While this is unlikely, the probability of losing, for instance, in ten or twenty sessions is extremely small.

This article is not a how-to guide; instead, it offers food for thought. Feel free to explore the effectiveness of this system, and only after that should you consider playing for real money. Remember that gambling can be addictive and may have devastating effects on your life. If you are unsure whether you can resist gambling addiction, you should not attempt to gamble.
We have a request. If anyone chooses to try this betting system, please share your results in the comments section of the article below!